年金终值公式，复利年金终值公式

年金终值是指在一定期间内，按照固定的时间间隔（如每年、每季等）进行等额支付的年金，在期末累积到某一特定时间点的价值。它是评估长期投资回报和财务规划的重要工具。

1.普通年金终值公式解析

普通年金终值公式：F=A×(F/A,i,n)

-F表示年金终值；

A表示每期支付的金额；

(F/A,i,n)为普通年金终值系数，它可以通过查询普通年金终值系数表得到；

i表示每期的利率；

公式推导：

设每年的支付金额为A，利率为i，期数为n，则按复利计算的普通年金终值S为：

S=A+A×(1+i)+A×(1+i)^2+…+A×(1+i)^(n-1)

等式两边同乘以(1+i)：

S(1+i)=A(1+i)+A(1+i)^2+…+A(1+i)^n

上式两边相减可得：

S(1+i)-S=A(1+i)^n-A

S=A[(1+i)^n-1]/i

2.先付年金终值计算

先付年金终值公式：F=A×(F/A,i,n)×(1+i)

先付年金与普通年金的主要区别在于，先付年金的每期支付发生在期初，而普通年金的支付发生在期末。先付年金的终值需要额外乘以(1+i)。

3.递延年金终值公式

递延年金终值公式：F=A×(F/A,i,n)

递延年金是指在一定期间内没有支付，之后才开始支付的年金。递延年金的终值计算与普通年金相同，只需将期数n调整为递延年金中A的个数。

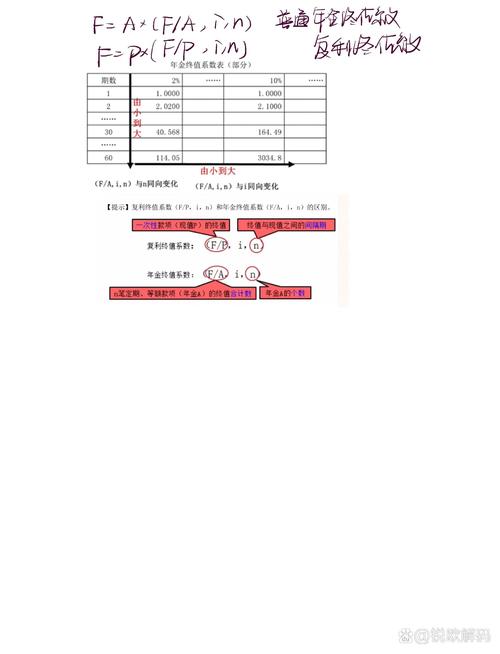
4.年金终值系数表

由于每年支付额相等，折算终值的系数又是有规律的，因此可以通过查询年金终值系数表来简化计算。年金终值系数表列出了不同利率和期数下的年金终值系数。

5.年金终值公式应用

年金终值公式是根据出发金额（本金）、投资收益率（利率）和期间单位时间（期数）来计算投资期末时的现金价值（终值）的方法。它广泛应用于财务规划、投资评估和退休规划等领域。

6.复利终值与普通年金终值

复利终值：F=×(1+i)^n

普通年金终值：F=A×(F/A,i,n)

两者之间的区别在于，复利终值计算的是单次支付的本利和，而普通年金终值计算的是一系列等额支付的终值。

通过以上对年金终值公式的解析和应用，我们可以更好地理解和运用这一金融工具，为个人和企业的财务决策提供有力支持。